DEVELOPMENT OF A NEW BULLET TRAP DESIGN USING SHOCK-ABSORBING CONCRETE (SACON™)
B. L. Huntsman* and B. E. Huntsman
Terran Corporation
Beavercreek, OH 45430-1061
P. G. Malone, J. G. Tom, and C. A. Weiss Jr.
U. S. Army Engineer Research and Development Center
Vicksburg, MS 39180-6199
ABSTRACT
A variety of bullet traps are currently being marketed for use on small arms training ranges. Generally they can be classed as deceleration traps (such as the steel drum or snail trap), deflection traps (typically angled steel plates over a sand bed) or ablation traps (such as foamed concrete blocks or rubber blocks). Deceleration or deflection traps often grind and pulverize the incoming bullet. High volume air filtration systems must be used to assure particulate lead does not escape from the trap. Rubber ablation traps are problematic in that they can burn with devastating consequences. Also, any drainage from the trap area may contain organics from the rubber and heavy metals from the bullet fragments. Material from the rubber traps must be treated as a hazardous waste when it leaves the range.
A new bullet trap has been developed that is fabricated entirely from blocks of foamed, fiber-reinforced concrete commonly called shock-absorbing concrete (SACON™*). It combines the best aspects of the SACON™ block bullet barriers with deflection technology to produce a trap that has improved safety, security and containment for spent bullets. The new design consists of a stack of SACON™ tapered, log-like elements. The cylindrical or log-like elements are typically six inches in diameter and four feet long with the point end directed toward the shooter. The logs are manufactured using 90 lbs per cubic foot foamed concrete and weigh approximate 60 lbs each. The incoming bullet strikes the log-stacks at a low angle of impact. The bullet either imbeds itself into the element or ricochets into the space between the logs and passes through the log-stack to impact on a SACON™ block backstop. Spent bullets and debris from the log-stack accumulates in the space between the log “screen” and the block backstop wall. This design provides for trap maintenance while restricting unauthorized personnel from access to the bullet debris.
The foamed concrete is manufactured using crushed limestone sand with a calcium phosphate additive . The alkalinity of the sand and the availability of the phosphate to react with and passivate the surfaces of the metal fragments reduce the amount of lead that will leach from the debris. The trap is completely modular and can be assembled in almost any space where a suitable footing can be prepared. By design, these traps are vandal and varmint resistant, require minimal maintenance and are recyclable.
* SACON™ is a trademark of the U.S. Army Corps of Engineers.
1. INTRODUCTION
Most bullet traps marketed today involve designs that use steel and/or rubber as rubber belts (lamellae traps), granular rubber or rubber blocks (TRW. Inc, 1996). Having any steel structure in front of the shooter has the inherent risk of producing a deadly ricochet. Unfortunate examples include an accident in which a Marine machinegun tripod slipped and the fire was directed into a metal deck. The resulting ricochet wounded a lance corporal and a sergeant (Troutman, 1995). A pistol bullet ricocheted during a training session and wounded an Orange County, CA police recruit in the neck and shoulder (Leonard, 1999). Border patrol officers have reported being hit by ricochets during close-in pistol training with drop-down steel targets.
The steel target manufacturers admit to having a "splatter zone" that extends as a cone approximately 20 degrees out from the point where the line of fire intersects the face of the steel plate. The distance that bullet splatter (fragments) will travel depends of the ability of the bullet to breakup into a cloud of metal dust when it hits the steel. However, many modern bullets are designed to prevent total fragmentation. The M855 round contains a steel penetrator, guaranteeing at least one lethal fragment will survive an impact with steel.
Discharging any weapon against a steel structure (even a "reactive target") can present a serious ricochet hazard to all personnel on the range. The angled surfaces of steel bullet traps are designed to deflect a bullet so the ricochet will land or be captured harmlessly. In many cases the steel supporting structures around steel or rubber traps cannot be angled, requiring the use of wood or rubber appliques in an attempt to protect the shooter (see Figure 1). Ideally all exposed surfaces that are in front of the shooter (target holders, targets and bullet traps) should be made from durable materials that will not produce ricochets.

Figure 1. A rubber belt trap with rubber strips (red) protecting the steel beams supporting the hanging belts. The cover strips must be routinely inspected and maintained to prevent ricochets (white arrows pointing to exposed steel from bullet holes). Tracers cannot be used in this trap.
A second disadvantage with steel bullet traps is bullets that impact, deform and fragment create significant amounts of metal dust. Lead dust can be present around a metal trap in quantities that exceed the health and safety thresholds. Attempts to control metal dust by forced ventilation in the trap may be unsuccessful due to the reduced air velocity at the wide end of any tapering metal trap. Additionally the dust frequently is being ejected from the trap due to rebound from the bullet impacting on the steel. Over time, metal dust and debris will contaminate the soil in front of a steel trap.
Rubber traps (rubber blocks, rubber belts or shredded rubber) can capture bullets with a lower probability of producing small bullet fragments when compared to metal traps. However, the combination of rubber, spent lead bullets and bullet fragments will always be classified as a hazardous waste. This is due to the rubber matrix contributing organic compounds while not preventing the leaching of metals from the spent bullets during testing for waste characterization. Additionally there is always the problem of the rubber traps becoming involved in a fire. If a tracer round, deflagrating bullets or any other accidental source ignites a rubber trap, there are no guarantees that the fire will self-extinguish. The combustion of rubber produces other waste materials, some which are carcinogens. Even a small rubber trap fire can produce significant contamination of equipment and soil on the range. In the event of a rubber fire, all of the debris and even the water used to extinguish the fire has to be considered a hazardous waste.
Currently, the best alternate material for use in bullet traps is foamed, fiber-reinforced concrete (also referred to as shock-absorbing concrete or SACON™). In its basic form, SACON™ is a mixture of sand, Portland cement, fiber and aqueous-based foam. Physically, SACON™ has a density of approximately one-half and an unconfined compressive strength about one-third that of conventional concrete. The closed cellular structure and the large quantity of fiber (typically 16-lbs/cubic yd. of concrete) impart wood-like characteristics to this foamed mortar mixture. It dents when struck with a hammer and bullets fired directly into blocks punch clean holes, crushing the SACON™ without producing cracking or ricochets. Like commercial cement board, (another fiber-reinforced mortar product), SACON™ is moisture-proof, fireproof, and cannot be damaged by mold or insects. It can be cast into almost any shape and colored with pigment or paint.
Materials used in SACON™ prevent lead leaching from spent bullets into the environment (Tom, et al, 1997; Malone et al, 1997). SACON™ contains calcium hydroxide that is generated from the hydration of the calcium silicate in the cement. The preferred aggregate is crushed limestone (calcium carbonate). These compounds react with any acidic components in the environment to maintain a pH above 7.0 (Sigurdson et al, 1997). Calcium phosphate can be added to the mixture to further assist in preventing lead from leaching by forming a non-reactive coating of metal phosphate on the exposed surfaces of the bullet fragments. The high buffer capacity of the debris from SACON™ and the passivation of the exposed metal surfaces keeps the mixture of foamed concrete and bullet fragments from leaching lead at a level that would be considered hazardous to the environment. Waste SACON™ can generally be disposed of in a conventional landfill after testing to establish that the material meets requirements established by local environmental authorities (Fabian et al, 1998). If the value of the metal present is sufficient to justify shipping the material to a smelter for recycling, it is typically not necessary to separate the concrete and the metal fragments. The concrete fragments become a flux when the scrap is sent into the furnace.
2. DESIGN OF SACON™ BULLET TRAPS
The earliest attempts to use fiber-reinforced concrete as a bullet trapping medium involved building a wall of block directly behind a target (Fabian et al, 1996, 1997). Debris created by the impact of the bullets on the barrier accumulated at the foot of the wall (Figure 2). This material could be collected and discarded or recycled. Some drawbacks to this simple approach included easy access to the bullet debris by scavengers and the disposal of dust generated from the bullet impacts was dispersed. There was a need for a new trap design that enclosed the debris so particulate material could not be scattered or scavenged. Further it was recognized if airflow could be controlled at the face of the trap, SACON™ traps could be used on indoor as well as outdoor ranges.

Figure 2. Test bullet trapping SACON™ block wall in an open fiberglass-and-plastic shelter. The bullet debris is collected in a plastic tray at the base of the wall. The frame was assembled with nylon bolts to eliminate ricochets.
2.1 Grated or Screened Bullet Trap
The grated trap consists of a box-shaped structure made completely of SACON™ blocks and panels stacked on a packed earth foundation. Figure 3 illustrates the trap design. The entrance of the trap is filled with pre-cast bars or cylinders of SACON™ (the screen section). Screen shapes are selected that will create holes in the stack so that the incoming bullets will strike the ends of the elements and ricochet through the stack. If not contained in the screen material, the backstop blocks, in the back of the trap, stops the bullet. Impacts between the incoming bullets and the sides of the screen elements reduce the velocity of the bullet and reduce the amount of penetration the bullet can produce when it hits the blocks in the backstop. The loss of energy will depend on the angle at which the bullet impacts the sides of the grating blocks and the initial velocity and mass of the bullet. Figure 4 depicts typical velocity reductions produced by single impacts for a variety of military ammunition (Hudson et al, 1999). In the case of the M855 and the M193 rounds, any impact on the grating blocks will cause the bullet to tumble and reduce its ability to penetrate into the backstop blocks.
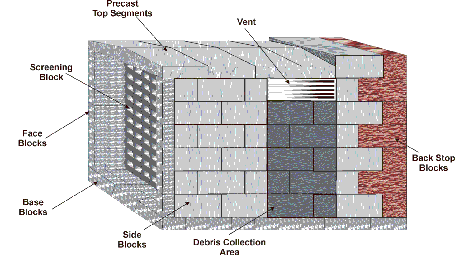
Figure 3. Schematic cross-section of the grated trap showing the position of the SACON™ screen elements, the backstop blocks, and the debris collection area is the space between the grating and the backstop.
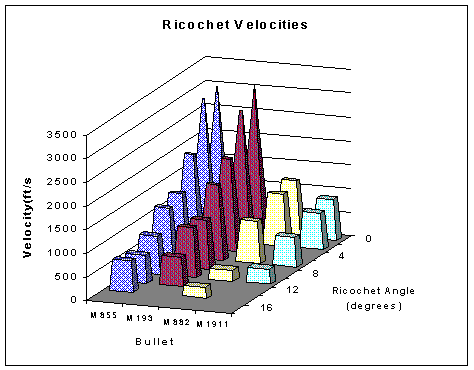
Figure 4. The reduction of velocity as a function of ricochet angle of various caliber bullets striking a SACON™ surface. (data from Hudson et al, 1999)
When this trap design is used indoors, a dust collection system can be installed to draw air from the back of the trap through the spaces between the elongate blocks in the grating. The velocity of the air moving behind the grating will be lower than the velocity of air in the spaces between the screening blocks. Air moving through the grating will decrease in velocity and dust from the grating blocks will be deposited between the grating and the backstop blocks. Dust produced by the impact of bullets on the front of the grating or screen will be drawn back into the trap and collected.
2.2 Dust and Debris Disposal
In the SACON™ grating , metal fragments are mixed with dust and debris from the shock-absorbing concrete. This mixture produces a waste product that has an alkaline pH and a very high buffering capacity. Furthermore, phosphate added to the mortar mixture will react with the lead particles to produce a surface coating of lead phosphate, one of the most insoluble lead compounds. Since the waste material will typically leach less lead than the threshold amount that defines hazardous wastes, both the coarse debris and the particles from the dust collection system should be acceptable for disposal as conventional non-hazardous wastes. Producing non-hazardous material greatly reduces health and safety concerns as well as the costs of handling and disposal.
2.3 Security and Metal Recycling
The new trap design is especially well suited to ranges where scrap metal scavenging cannot be permitted. The new trap design is a concrete bunker made with blocks and panels of foamed fiber-reinforced concrete. Bullet debris is contained between four concrete walls and concrete roof panels. Cleaning scrap metal out of the trap can only be done when the side panels are lifted out or the screen elements are disassembled.
3. Conclusions
Using readily available pre-cast blocks of SACON™, a new bullet trap design has been developed which provides many advantages over the standard steel or rubber traps in common use. SACON™ traps have been shown to:
- Minimize ricochets, with less bullet fragmentation and greater energy loss at low angles of bullet impact,
- Provide an effective firing zone of nearly 140o to the face of the trap, freeing the shooter from a fixed firing position,
- Retain spent bullets and bullet debris within the trap in a more environmentally safe manner while allowing the material to be recycled or disposed as non-hazardous waste,
- Allow bullet trap construction in modular sections without using heavy equipment, resulting in easy maintenance with troop labor,
- Reduce life-cycle costs when compared to conventional bullet trap designs of steel or rubber.
References
Fabian, G. L., Lee, L. T., Malone, P. G., and Tom, J. G., “Design of modular bullet-trapping units using shock-absorbing concrete (SACON)”, D. Bader, Proceedings of the Second Tri-Services Environmental Research and Development Workshop, Publ. No. SFIM-AEC-ET-CR-97050, U.S. Army Environmental Center, Aberdeen Proving Ground, MD, pp. 129-137, 1997.
Fabian, G. L., O'Donnell, R. H., Tom, J. G., and Malone, P. G, “Use of shock-absorbing concrete (SACON) as an environmentally compatible bullet-trapping medium on small-arms training ranges”, D. Bader, Proceedings of the Tri-Services Environmental Research and Development Workshop, Publ. No. SFIM-AEC-ET-CR-96187, U.S. Army Environ-mental Center, Aberdeen Proving Ground, MD, pp. 187-196, 1996.
Fabian, G. L., Tom, J. G., and Malone, P. G., “Recycling shock-absorbing concrete (SACON) bullet barriers”, 24th Environmental Symposium and Exhibition, Tampa, Florida, National Defense Industrial Association, Arlington, VA., April 6-9, 1998.
Hudson, K. L., Fabian, G. L., and Malone, P. G., “Demonstration of Shock Absorbing Concrete (SACON) Bullet Trap Technology”, USAEC Report No. SFIM-AEC-ET-CR-99017, 195 p., 1999.
Leonard, Jack, “Instructor accidentally wounds recruit”, Los Angeles Times, Archive No. 0990104848, November 17, 1999.
Malone, P. G., Brabston, W. N., and Tom, J. G., “SACON barriers”, The Military Engineer 89(586), pp. 34-35, 1997.
Sigurdson, J., Malone, P. G., Tom, J. G., and Fabian, G. L., “Management of spent bullets and bullet debris on training ranges using shock-absorbing concrete (SACON)” 1997 Waste Management Conference, Portland, Oregon, American Defense Preparedness Association, Arlington, VA., January 27-28, 1997.
Tom, J. G., Malone, P. G., Bean, D. L., and Fabian, G. L., “Chemical containment of heavy metals from bullet debris in shock-absorbing concrete (SACON) bullet barriers” 23rd Environmental Symposium and Exhibition, American Defense Preparedness Association, Arlington, VA, pp. 79-83, 1997.
Tom, J. G., Berger, R. P., and Malone, P. G., “Design of bullet traps using foamed, fiber-reinforced concrete”, 67th Shock and Vibration Symposium, Monterey, CA., November 18-22, 1996.
Troutman, Bob, “Watch that ricochet!”, Fathom, Vol. 27, No. 4, 30 p., 1995.
TRW, Inc., “Bullet trap feasibility assessment and implementation plan”, Technology Identification, Report No. SFIM-ET-CR-96005, U.S. Army Environmental Center, Aberdeen Proving Ground, MD, 94 p., 1996.
This paper was presented at the following symposium and it is published in the symposium proceedings:
Fourth Tri-Service Environmental Technology Symposium
June 18-20, 2001
San Diego, California
